- 水壶问题
- 描述
- 分析
- 源码
- 链表的中间结点
- 描述
- 分析
- 车的可用捕获量
- 描述
- 分析
- 代码
- 卡牌分组
- 描述
- 分析
- 代码
- 单词的压缩编码
- 描述
- 分析
- 代码
- 地图分析
- 描述
- 分析
- 代码
- 圆圈中最后剩下的数字
- 描述
- 分析
- 代码
- 有效括号的嵌套深度
- 描述
- 分析
- 代码
- 生命游戏
- 描述
- 分析
- 代码
- 字符串转换整数 (atoi)
- 描述
- 分析
- 代码
- LFU 缓存
- 描述
- 分析
- 代码
- 旋转矩阵
- 描述
- 分析
- 代码
- 机器人的运动范围
- 描述
- 分析
- 代码
- 括号生成
- 描述
- 分析
- 代码
- 翻转字符串里的单词
- 描述
- 代码
- 鸡蛋掉落
- 描述
- 代码
- 设计推特
- 描述
- 代码
- 两数相加 II
- 描述
- 分析
- 代码
- 01 矩阵
- 描述
- 分析
- 代码
- 合并区间
- 描述
- 分析
- 代码
- 跳跃游戏
- 描述
- 分析
- 代码
- 盛最多水的容器
- 描述
- 分析
- 代码
- 岛屿数量
- 描述
- 分析
- 代码
- 统计「优美子数组」
- 描述
- 分析
- 代码
- 二叉树的右视图
- 描述
- 分析
- 代码
- 硬币
- 描述
- 分析
- 代码
- 数组中的逆序对
- 描述
- 分析
- 代码
- 合并 K 个排序链表
- 描述
- 分析
- 代码
- 搜索旋转排序数组
- 描述
- 分析
- 代码
- 代码二
- 数组中数字出现的次数
- 描述
- 分析
- 代码
- 山脉数组中查找目标值
- 描述
- 分析
- 代码
- 快乐数
- 描述
- 分析
- 代码
水壶问题
描述
有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 z升 的水?
如果可以,最后请用以上水壶中的一或两个来盛放取得的 z升水。
你允许:
- 装满任意一个水壶
- 清空任意一个水壶
- 从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1: (From the famous "Die Hard" example)
输入: x = 3, y = 5, z = 4输出: True
示例 2:
输入: x = 2, y = 6, z = 5输出: False
分析
首先我们要明确一点,每次操作仅仅会让桶中水的总量增加 x 或增加 y,减少或减少 y。
因为在题目给定的条件下,两个桶不存在都有水并且都不满的情况,换言之,操作后,两个桶中水至少一个是空或者满。再者,我们分析易知:对一个不满的桶加水是没有什么意义的,为什么呢?因为给一个不满的桶加水其实就相当于将该桶初始化为满桶水;同理将一个未装满水桶的水倒掉也没有意义。
通过分析我们还能得出,两桶水的总量是否能满足给定的 z 是取决于 x、y 两桶容量的差值,也就是说差的制造是通过反复将大桶中的水倒入小桶产生的,整个操作描述如下:
往 y 壶倒水
把 y 壶的水倒入 x 壶
如果 y 壶不为空,那么 x 壶肯定是满的,把 x 壶倒空,然后再把 y 壶的水倒入 x 壶
重复以上操作直至某一步时 x 壶进行了 m 次倒空操作,y 壶进行了 n 次倒水操作。
由贝祖定理可得:mx+ny=z,当且仅当 z 是 x、y 最大公约数的倍数时,成立,因此,我们只需找出 x、y 最大公约数即可。
源码
/*** @param {number} x* @param {number} y* @param {number} z* @return {boolean}*/var canMeasureWater = function(x, y, z) {if (x + y < z) {return false;}if (x === 0 || y === 0) {return z === 0 || x + y === z;}return z % calcGcd(x, y) === 0;};function calcGcd(a, b) {if (b === 0) {return a;}return calcGcd(b, a % b);}
链表的中间结点
描述
给定一个带有头结点 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例 1:
输入:[1,2,3,4,5]输出:此列表中的结点 3 (序列化形式:[3,4,5])返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。注意,我们返回了一个 ListNode 类型的对象 ans,这样:ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2:
输入:[1,2,3,4,5,6]输出:此列表中的结点 4 (序列化形式:[4,5,6])由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
提示:
- 给定链表的结点数介于 1 和 100 之间。
分析
该问题有几种思路:
因为链表没有下标,因此该题需要遍历链表。
方法一:数组
遍历数组的同时,将元素放入数组,然后取出数组中间元素,但是会有内存额外开销,时间复杂度
- 时间复杂度:O(N)O(N),其中 NN 是给定链表中的结点数目。
- 空间复杂度:O(N)O(N),即数组
A用去的空间。
方法二:单指针法
对数组进行两次遍历,第一次统计链表长度,计算出中间位置索引,进行第二次遍历返回中间链表节点
/*** Definition for singly-linked list.* function ListNode(val) {* this.val = val;* this.next = null;* }*//*** @param {ListNode} head* @return {ListNode}*/var middleNode = function(head) {let linkSize = 0;let current = head;while (current) {++linkSize;current = current.next;}let currentIndex = 0;const middleIndex = Math.floor(linkSize / 2);current = head;while (currentIndex < middleIndex) {++currentIndex;current = current.next;}return current;};
- 时间复杂度:O(N)O(N),其中 NN 是给定链表的结点数目。
- 空间复杂度:O(1)O(1),只需要常数空间存放变量和指针。
快慢指针法
用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步,fast 一次走两步。那么当 fast 到达链表的末尾时,slow 必然位于中间。
var middleNode = function(head) {slow = fast = head;while (fast && fast.next) {slow = slow.next;fast = fast.next.next;}return slow;};
- 时间复杂度:O(N)O(N),其中 NN 是给定链表的结点数目。
- 空间复杂度:O(1)O(1),只需要常数空间存放
slow和fast两个指针。
车的可用捕获量
描述
在一个 8 x 8 的棋盘上,有一个白色车(rook)。也可能有空方块,白色的象(bishop)和黑色的卒(pawn)。它们分别以字符 “R”,“.”,“B” 和 “p” 给出。大写字符表示白棋,小写字符表示黑棋。
车按国际象棋中的规则移动:它选择四个基本方向中的一个(北,东,西和南),然后朝那个方向移动,直到它选择停止、到达棋盘的边缘或移动到同一方格来捕获该方格上颜色相反的卒。另外,车不能与其他友方(白色)象进入同一个方格。
返回车能够在一次移动中捕获到的卒的数量。
示例 1:

输入:[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]输出:3解释:在本例中,车能够捕获所有的卒。
示例 2:

输入:[[".",".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]输出:0解释:象阻止了车捕获任何卒。
示例 3:

输入:[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]]输出:3解释:车可以捕获位置 b5,d6 和 f5 的卒。
提示:
- board.length == board[i].length == 8
- board[i][j] 可以是 'R','.','B' 或 'p'
- 只有一个格子上存在 board[i][j] == 'R'
分析
没下过国际象棋,题目有读不懂,放弃!
其实,描述说的问题我们通过图来说明,以白色车为原点,向上下、左右试探。

所以我们首先找到白色车所在位置,然后遍历获取到 X 向、Y 向数组,并且过滤掉空白块,得到的数组我们只需要从第一个"p"开始找,到下一个"p"或者墙结束
代码
/*** @param {character[][]} board* @return {number}*/var numRookCaptures = function(board) {let y,xlist = [],ylist = [],boardXLen = 8;for (let i = 0; i < boardXLen; i++) {if (board[i].indexOf('R') > -1) {y = board[i].indexOf('R');xlist = board[i].filter(e => e !== '.');}}for (let i = 0; i < boardXLen; i++) {board[i][y] !== '.' && ylist.push(board[i][y]);}let rx = xlist.indexOf('R'),ry = ylist.indexOf('R'),num = 0;if (xlist[rx + 1] && xlist[rx + 1] === 'p') ++num;if (xlist[rx - 1] && xlist[rx - 1] === 'p') ++num;if (ylist[ry + 1] && ylist[ry + 1] === 'p') ++num;if (ylist[ry - 1] && ylist[ry - 1] === 'p') ++num;return num;};
卡牌分组
描述
给定一副牌,每张牌上都写着一个整数。
此时,你需要选定一个数字 X,使我们可以将整副牌按下述规则分成 1 组或更多组:
每组都有 X 张牌。
组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。
示例 1:
输入:[1,2,3,4,4,3,2,1]输出:true解释:可行的分组是 [1,1],[2,2],[3,3],[4,4]
示例 2:
输入:[1,1,1,2,2,2,3,3]输出:false解释:没有满足要求的分组。
示例 3:
输入:[1]输出:false解释:没有满足要求的分组。
示例 4:
输入:[1,1]输出:true解释:可行的分组是 [1,1]
示例 5:
输入:[1,1,2,2,2,2]输出:true解释:可行的分组是 [1,1],[2,2],[2,2]
提示:
1 <= deck.length <= 100000 <= deck[i] < 10000
分析
我们发现每个数组必须满足以下条件:
- 相同牌的个数必须大于 2
- 不同牌个数可以拆分为相同个数的小组,这点非常关键
为了好记录每张牌的张数,使用 Map 来存放数据。然后获取到存放张数的数组,保证每一项与前一项的最大公约数都大于 1。
代码
/*** @param {number[]} deck* @return {boolean}*/var hasGroupsSizeX = function(deck) {let m = new Map();for (let n of deck) {m.set(n, m.has(n) ? m.get(n) + 1 : 1);}const vals = [...m.values()];let res = vals[0];return vals.every(val => (res = calcGcd(res, val)) > 1);};function calcGcd(a, b) {return b === 0 ? a : calcGcd(b, a % b);}
单词的压缩编码
描述
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 ["time", "me", "bell"],我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。
对于每一个索引,我们可以通过从字符串 S 中索引的位置开始读取字符串,直到 "#" 结束,来恢复我们之前的单词列表。
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
提示:
1 <= words.length <= 2001 <= words[i].length <= 7- 每个单词都是小写字母 。
分析
方法一:遍历后缀,hash 检索
我们将数据存放在一个容器中,然后逐个拿出,检测拿出的字符串是否存在后缀在原容器中,如果存在,则删除,不存在则继续查看更小后缀,直至对比完该字符串,转而从容器拿出下一个元素,直至所有元素均检测完,处理并返回结果。
这个容器是散列集合 Set ,动画演示,转自LeetCode

时间复杂度:
其中 w_i 是 words[i] 的长度
空间复杂度:
方法二:Trie/字典树/前缀树
关于前缀树算法题,可见:LeetCode208. 实现 Trie (前缀树)
假设我们现在给定字符串数组:"A", "to", "tea", "ted", "ten", "i", "in", "inn"

这颗树怎么理解呢?根节点无内容,读取第一个元素 A 加入这颗树,结果为:{A: {}},读取第二个字符串 to ,构造出 {t:{o:{}}, A:{}},继续读取第三个元素,构造出:{t:{o:{}, e: {a: {}}}, A:{}}。以此类推,将所有元素存放进树中。代码实现如下:
/*** 初始化树.*/var Trie = function() {this.root = {};};/*** 将元素添加到树汇总*/Trie.prototype.insert = function(word) {let cur = this.root;for (i = 0; i < word.length; i++) {const char = word.charAt(i);if (!cur[char]) {cur[char] = {};}cur = cur[char];}cur.isWord = true;};/*** 搜索树中是否含有某给定字符串*/Trie.prototype.search = function(word) {let cur = this.root;for (i = 0; i < word.length; i++) {const char = word.charAt(i);if (!cur[char]) {return false;}cur = cur[char];}return cur.isWord || false;};/*** 搜索树中是否含有以给定字符串为前缀*/Trie.prototype.startsWith = function(prefix) {let cur = this.root;for (i = 0; i < prefix.length; i++) {const char = prefix.charAt(i);if (!cur[char]) {return false;}cur = cur[char];}return true;};
有了前缀树的概念,我们再来解这道题似乎很简单了。
针对本题,我们不是看各字符串的公共前缀,而是看后缀,怎么理解呢?我们看一张图,转自LeetCode
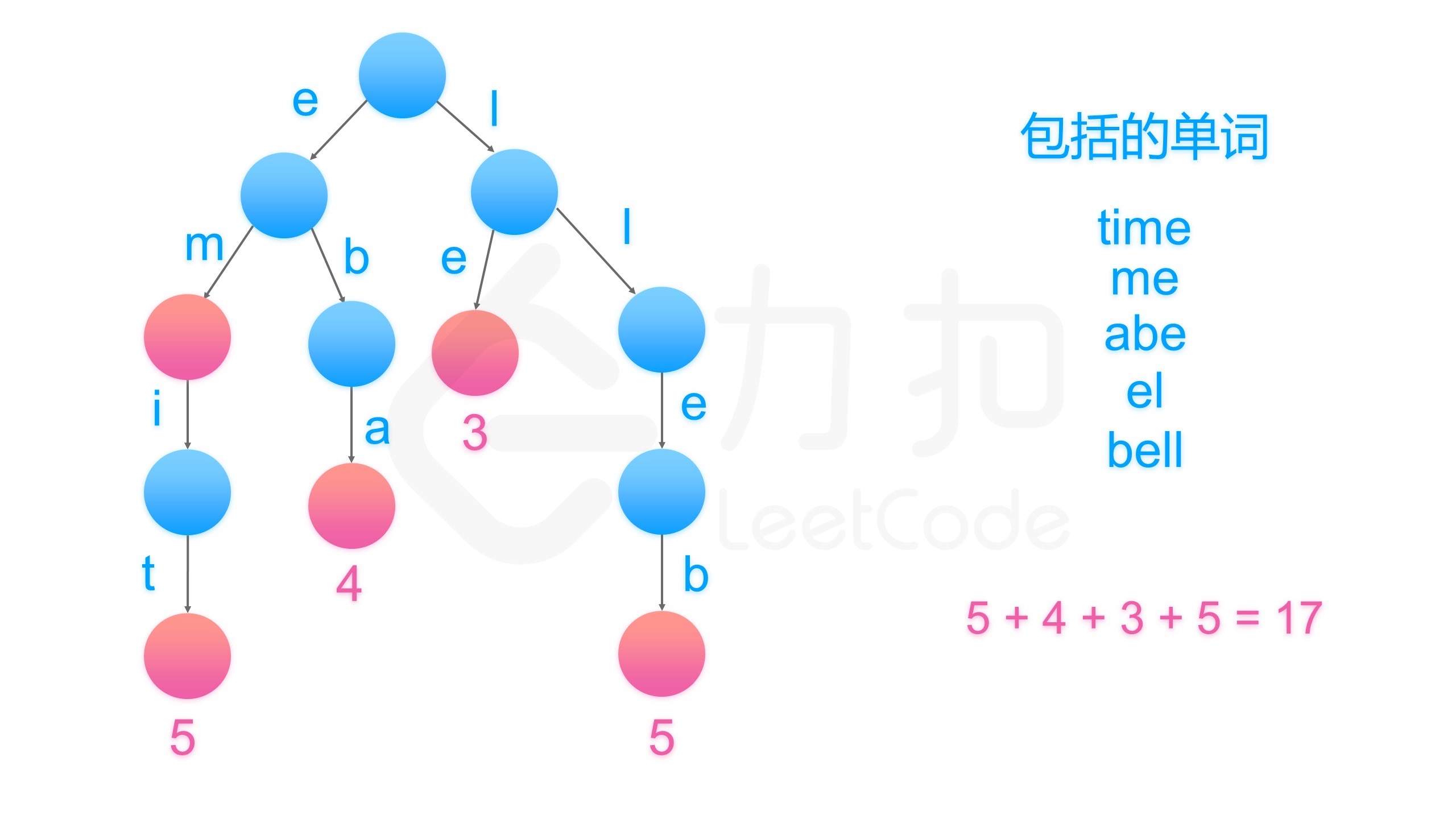
我们把所有字符串先反转,然后存到字典树,查找时,我们只用统计根节点到叶子节点的节点个数+1 的总和,即可知道字符串压缩后的长度
代码
方法一:遍历后缀,hash 检索
/*** @param {string[]} words* @return {number}*/var minimumLengthEncoding = function(words) {const wordSet = new Set(words);for (let word of words) {for (let i = 1; i < word.length; i++) {wordSet.delete(word.substring(i));}}return [...wordSet].join('#').length + 1;};
方法二:Trie/字典树/前缀树
/*** @param {string[]} words* @return {number}*/var minimumLengthEncoding = function(words) {const trie = new Trie();let len = 0;const cwords = words.sort((a, b) => b.length - a.length);for (let word of cwords) {len += trie.insert(word);}return len;};var Trie = function() {this.root = {};};Trie.prototype.insert = function(word) {let cur = this.root;let isNew = false;for (i = word.length - 1; i >= 0; i--) {const char = word.charAt(i);if (!cur[char]) {isNew = true;cur[char] = {};}cur = cur[char];}return isNew ? word.length + 1 : 0;};
地图分析
描述
你现在手里有一份大小为 N x N 的『地图』(网格) grid,上面的每个『区域』(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,你知道距离陆地区域最远的海洋区域是是哪一个吗?请返回该海洋区域到离它最近的陆地区域的距离。
我们这里说的距离是『曼哈顿距离』( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。
如果我们的地图上只有陆地或者海洋,请返回 -1。
示例 1

输入:[[1,0,1],[0,0,0],[1,0,1]]输出:2解释:海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大,最大距离为 2。
示例 2

输入:[[1,0,0],[0,0,0],[0,0,0]]输出:4解释:海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大,最大距离为 4。
提示:
1 <= grid.length == grid[0].length <= 100grid\[i][j]不是0就是1
分析
本题实现方法很多,可使用 宽度优先搜索、多源最短路、动态规划
多源最短路的示例图,引自LeetCode

我们知道对于每个海洋区域 (x, y)(x,y),离它最近的陆地区域到它的路径要么从上方或者左方来,要么从右方或者下方来。考虑做两次动态规划,第一次从左上到右下,第二次从右下到左上,记 f(x, y)f(x,y) 为 (x, y)(x,y) 距离最近的陆地区域的曼哈顿距离,则我们可以推出这样的转移方程:

我们初始化的时候把陆地的 f 值全部预置为 0,海洋的 f 全部预置为 INF,做完两个阶段的动态规划后,我们在所有的不为零的 f[i][j] 中比一个最大值即可,如果最终比较出的最大值为 INF,就返回 -1。
代码
/*** @param {number[][]} grid* @return {number}*/var maxDistance = function(grid) {if (grid.length < 2) return -1;let n = grid.length;// 创建 dp 状态矩阵let dp = new Array(n);for (let i = 0; i < n; i++) {dp[i] = new Array(n);}for (let i = 0; i < n; i++) {for (let j = 0; j < n; j++) {dp[i][j] = grid[i][j] ? 0 : Infinity;}}// 从左上向右下遍历for (let i = 0; i < n; i++) {for (let j = 0; j < n; j++) {if (grid[i][j]) continue;if (i - 1 >= 0) dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + 1);if (j - 1 >= 0) dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + 1);}}// 从右下向左上遍历for (let i = n - 1; i >= 0; i--) {for (let j = n - 1; j >= 0; j--) {if (grid[i][j]) continue;if (i + 1 < n) dp[i][j] = Math.min(dp[i][j], dp[i + 1][j] + 1);if (j + 1 < n) dp[i][j] = Math.min(dp[i][j], dp[i][j + 1] + 1);}}let ans = -1;for (let i = 0; i < n; i++) {for (let j = 0; j < n; j++) {if (!grid[i][j]) ans = Math.max(ans, dp[i][j]);}}if (ans === Infinity) {return -1;} else {return ans;}};
圆圈中最后剩下的数字
描述
0,1,,n-1 这 n 个数字排成一个圆圈,从数字 0 开始,每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4 这 5 个数字组成一个圆圈,从数字 0 开始每次删除第 3 个数字,则删除的前 4 个数字依次是 2、0、4、1,因此最后剩下的数字是 3。
示例 1
输入: n = 5, m = 3输出: 3
示例 2
输入: n = 10, m = 17输出: 2
限制
1 <= n <= 10^51 <= m <= 10^6
分析
著名约瑟夫环问题,可以使用递归实现,但是有存在堆栈溢出问题。分析规律可以使用循环解决。
我们以 n=5, m=3为例

很明显我们每次删除的是第 mm 个数字,我都标红了。
第一轮是 [0, 1, 2, 3, 4] ,所以是 [0, 1, 2, 3, 4] 这个数组的多个复制。这一轮 2 删除了。
第二轮开始时,从 3 开始,所以是 [3, 4, 0, 1] 这个数组的多个复制。这一轮 0 删除了。
第三轮开始时,从 1 开始,所以是 [1, 3, 4] 这个数组的多个复制。这一轮 4 删除了。
第四轮开始时,还是从 1 开始,所以是 [1, 3] 这个数组的多个复制。这一轮 1 删除了。
最后剩下的数字是 3。
图中的绿色的线指的是新的一轮的开头是怎么指定的,每次都是固定地向前移位 m 个位置。
然后我们从最后剩下的 3 倒着看,我们可以反向推出这个数字在之前每个轮次的位置。
最后剩下的 3 的下标是 0。
第四轮反推,补上 m 个位置,然后模上当时的数组大小 2,位置是 (0 + 3) % 2 = 1。
第三轮反推,补上 m 个位置,然后模上当时的数组大小 3,位置是 (1 + 3) % 3 = 1。
第二轮反推,补上 m 个位置,然后模上当时的数组大小 4,位置是 (1 + 3) % 4 = 0。
第三轮反推,补上 m 个位置,然后模上当时的数组大小 5,位置是 (0 + 3) % 5 = 3。
所以最终剩下的数字的下标就是 3。因为数组是从 0 开始的,所以最终的答案就是 3。
总结一下反推的过程,就是 (当前index + m) % 上一轮剩余数字的个数。
复杂度分析
- 时间复杂度:O(n)O(n),需要求解的函数值有
n个。 - 空间复杂度:O(1)O(1),只使用常数个变量。
代码
/*** @param {number} n* @param {number} m* @return {number}*/var lastRemaining = function(n, m) {let res = 0;for (let i = 2; i != n + 1; ++i) res = (m + res) % i;return res;};
有效括号的嵌套深度
描述
有效括号字符串 定义:对于每个左括号,都能找到与之对应的右括号,反之亦然。详情参见题末 **「有效括号字符串」**部分。
嵌套深度 depth 定义:即有效括号字符串嵌套的层数,depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末**「嵌套深度」**部分。
有效括号字符串类型与对应的嵌套深度计算方法如下图所示:

给你一个「有效括号字符串」 seq,请你将其分成两个不相交的有效括号字符串,A 和 B,并使这两个字符串的深度最小。
- 不相交:每个
seq[i]只能分给A和B二者中的一个,不能既属于A也属于B。 A或B中的元素在原字符串中可以不连续。A.length + B.length = seq.length- 深度最小:
max(depth(A), depth(B))的可能取值最小。
划分方案用一个长度为 seq.length 的答案数组 answer 表示,编码规则如下:
answer[i] = 0,seq[i]分给A。answer[i] = 1,seq[i]分给B。
如果存在多个满足要求的答案,只需返回其中任意 一个 即可。
示例 1
输入:seq = "(()())"输出:[0,1,1,1,1,0]
示例 2
输入:seq = "()(())()"输出:[0,0,0,1,1,0,1,1]解释:本示例答案不唯一。按此输出 A = "()()", B = "()()", max(depth(A), depth(B)) = 1,它们的深度最小。像 [1,1,1,0,0,1,1,1],也是正确结果,其中 A = "()()()", B = "()", max(depth(A), depth(B)) = 1 。
提示
1 <= text.size <= 10000
有效括号字符串:
仅由 "(" 和 ")" 构成的字符串,对于每个左括号,都能找到与之对应的右括号,反之亦然。下述几种情况同样属于有效括号字符串:1. 空字符串2. 连接,可以记作 AB(A 与 B 连接),其中 A 和 B 都是有效括号字符串3. 嵌套,可以记作 (A),其中 A 是有效括号字符串
嵌套深度:
类似地,我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S):1. s 为空时,depth("") = 02. s 为 A 与 B 连接时,depth(A + B) = max(depth(A), depth(B)),其中 A 和 B 都是有效括号字符串3. s 为嵌套情况,depth("(" + A + ")") = 1 + depth(A),其中 A 是有效括号字符串例如:"","()()",和 "()(()())" 都是有效括号字符串,嵌套深度分别为 0,1,2,而 ")(" 和 "(()" 都不是有效括号字符串。
分析
这道题其实主要在审题,代码如下挺简单,新匹配到括号则++然后%2,否则--然后%2。
代码
/*** @param {string} seq* @return {number[]}*/let maxDepthAfterSplit = (seq, dep = 0) => {return seq.split('').map(e => (e === '(' ? dep++ % 2 : --dep % 2));};
生命游戏
描述
根据 百度百科 ,生命游戏,简称为生命,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态:1 即为活细胞(live),或 0 即为死细胞(dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
根据当前状态,写一个函数来计算面板上所有细胞的下一个(一次更新后的)状态。下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。
示例 1
输入:[[0,1,0],[0,0,1],[1,1,1],[0,0,0]]输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
分析
这道题题意是:扫描一个数字,看他附近的 8 个元素(可能没有 8 个),分别对应以上列出的 4 个条件,更新数字。
代码
var gameOfLife = function(board) {let row = board.length;let col = board[0].length;let helper = function(ro, co, copy) {let count = 0;if (ro > 0) {count += copy[ro - 1][co];if (co > 0) {count += copy[ro - 1][co - 1];}if (co < col - 1) {count += copy[ro - 1][co + 1];}}if (ro < row - 1) {count += copy[ro + 1][co];if (co > 0) {count += copy[ro + 1][co - 1];}if (co < col - 1) {count += copy[ro + 1][co + 1];}}if (co > 0) {count += copy[ro][co - 1];}if (co < col - 1) {count += copy[ro][co + 1];}//根据状态进行归类,true为状态变化的,即死变活,活变死if (copy[ro][co] == 1) {if (count < 2) {return true;} else if (count > 3) {return true;}}if (copy[ro][co] == 0 && count == 3) return true;return false;};let copy = JSON.parse(JSON.stringify(board));for (let i = 0; i < row; i++) {for (let j = 0; j < col; j++) {if (helper(i, j, copy)) {//直接通过异或运算变更状态board[i][j] ^= 1;}}}};
字符串转换整数 (atoi)
描述
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。接下来的转化规则如下:
- 如果第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字字符组合起来,形成一个有符号整数。
假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成一个整数。
该字符串在有效的整数部分之后也可能会存在多余的字符,那么这些字符可以被忽略,它们对函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换,即无法进行有效转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0 。
示例 1
输入: "42"输出: 42
示例 2
输入: " -42"输出: -42解释: 第一个非空白字符为 '-', 它是一个负号。我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3
输入: "4193 with words"输出: 4193解释: 转换截止于数字 '3' ,因为它的下一个字符不为数字。
示例 4
输入: "words and 987"输出: 0解释: 第一个非空字符是 'w', 但它不是数字或正、负号。因此无法执行有效的转换。
示例 5
输入: "-91283472332"输出: -2147483648解释: 数字 "-91283472332" 超过 32 位有符号整数范围。因此返回 INT_MIN (−2^31) 。
分析
JavaScript 中提供该功能函数,parseInt 满足题目表述的需求。
我们分析,字符串首字符只能是数字、符号或空格,空格需要清除,然后逐步向后匹配满足为数字的字符,最终比较得到的数字是否超出 int 范围,如果超出则使用最大或最小 int 数。
代码
/*** @param {string} str* @return {number}*/var myAtoi = function(str) {str = str.trim();if (!/^[+|-]?\d+/.test(str)) return 0;let val = parseInt(str.match(/^[+|-]?\d+/));let base = Math.pow(2, 31);let min = -base,max = base - 1;return Math.max(Math.min(val, max), min);};
LFU 缓存
描述
设计并实现最不经常使用(LFU)缓存的数据结构。它应该支持以下操作:get 和 put。
get(key) - 如果键存在于缓存中,则获取键的值(总是正数),否则返回 -1。put(key, value) - 如果键不存在,请设置或插入值。当缓存达到其容量时,它应该在插入新项目之前,使最不经常使用的项目无效。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,最近最少使用的键将被去除。
进阶:
你是否可以在 O(1) 时间复杂度内执行两项操作?
示例
LFUCache cache = new LFUCache( 2 /* capacity (缓存容量) */ );cache.put(1, 1);cache.put(2, 2);cache.get(1); // 返回 1cache.put(3, 3); // 去除 key 2cache.get(2); // 返回 -1 (未找到key 2)cache.get(3); // 返回 3cache.put(4, 4); // 去除 key 1cache.get(1); // 返回 -1 (未找到 key 1)cache.get(3); // 返回 3cache.get(4); // 返回 4
分析
我们先回顾一下常用的缓存算法
LRU (Least recently used) 最近最少使用,如果数据最近被访问过,那么将来被访问的几率也更高。LFU (Least frequently used) 最不经常使用,如果一个数据在最近一段时间内使用次数很少,那么在将来一段时间内被使用的可能性也很小。FIFO (Fist in first out) 先进先出, 如果一个数据最先进入缓存中,则应该最早淘汰掉。
双 hash
一个存储数据,给定的 key 作为键,给定的 value、freq组成对象作为值;一个存储使用频率 freq 作为键,符合该频率的 key 组成数组作为值。
put 操作时,我们检测该值是否存在于 cache 中,若不存在则插入,并更新 freq,若存在,则直接更新 cache 、freq 。
get 操作获取值的同时,将该freq中该 key 频率数组+1 即可。
代码
/*** @param {number} capacity*/var LFUCache = function(capacity) {this.limit = capacity;this.cache = new Map();this.freqMap = new Map();};/*** @param {number} key* @return {number}*/LFUCache.prototype.get = function(key) {let cache = this.cache;let r = -1;if (typeof cache[key] != 'undefined') {let o = cache[key];r = o.value;//更新频率记录this.updateL(key, o);}return r;};/*** @param {number} key* @param {number} value* @return {void}*/LFUCache.prototype.put = function(key, value) {let { cache, limit, freqMap: fmap } = this;if (limit <= 0) return;if (typeof key == 'undefined' || typeof value == 'undefined')throw new Error('key or value is undefined');// 存在则直接更新if (typeof cache[key] == 'undefined') {// 获取频率 key// 判断容量是否满if (Object.keys(cache).length == limit) {let fkeys = Object.keys(fmap);let freq = fkeys[0];// 获取key集合let keys = fmap[freq];// 淘汰首位delete cache[keys.shift()];// delete cache[keys[0]];// keys.splice(0, 1);// 清理if (fmap[freq].length == 0) delete fmap[freq];}// 频率记录是否存在if (!fmap[1]) fmap[1] = [];// 插入新值fmap[1].push(key);cache[key] = {value: value,freq: 1, // 默认的频率};} else {cache[key].value = value;//更新频率记录this.updateL(key, cache[key]);}};LFUCache.prototype.updateL = function(key, obj) {let { freq } = obj;let arr = this.freqMap[freq];// 删除原频率记录this.freqMap[freq].splice(arr.indexOf(key), 1);// 清理if (this.freqMap[freq].length == 0) delete this.freqMap[freq];// 更新频率freq = obj.freq = obj.freq + 1;if (!this.freqMap[freq]) this.freqMap[freq] = [];this.freqMap[freq].push(key);};
旋转矩阵
描述
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1
给定 matrix =[[1,2,3],[4,5,6],[7,8,9]],原地旋转输入矩阵,使其变为:[[7,4,1],[8,5,2],[9,6,3]]
示例 2
给定 matrix =[[ 5, 1, 9,11],[ 2, 4, 8,10],[13, 3, 6, 7],[15,14,12,16]],原地旋转输入矩阵,使其变为:[[15,13, 2, 5],[14, 3, 4, 1],[12, 6, 8, 9],[16, 7,10,11]]
分析
二维数组的操作,并且要求 原地 操作,不能额外开辟空间。
双重循环,逐个先将 [i][j] 位置元素与 [j][i] 位置元素交换,最后将二维数组内层数组反转即可。
代码
/*** @param {number[][]} matrix* @return {void} Do not return anything, modify matrix in-place instead.*/let rotate = matrix => {for (let i = 0; i < matrix.length; i++) {for (let j = i; j < matrix[i].length; j++) {[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];}}matrix.forEach(row => row.reverse());};
机器人的运动范围
描述
地上有一个 m 行 n 列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如,当 k 为 18 时,机器人能够进入方格 [35, 37] ,因为 3+5+3+7=18。但它不能进入方格 [35, 38],因为 3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1
输入:m = 2, n = 3, k = 1输出:3
示例 2
输入:m = 3, n = 1, k = 0输出:1
提示:
1 <= n,m <= 1000 <= k <= 20
分析
很明显解题主要思路是 广度优先搜索 或者 深度优先搜索 ,一张图示例可以走通的位置,
m=20, n=15, k=9 的情况
转自 LeetCode

我们看到虽然右下角存在绿色方块,但是我们无法走到这些位置,因此最终可以走通的位置应该为

代码
/*** @param {number} m* @param {number} n* @param {number} k* @return {number}*/var movingCount = function(m, n, k) {let step = {};let num = 0;function dfs(i, j) {if (i < 0 || j < 0 || i >= m || j >= n) return;if (!step[`${i}|${j}`] && canMove(i, j, k)) {step[`${i}|${j}`] = true;num++;dfs(i - 1, j);dfs(i + 1, j);dfs(i, j - 1);dfs(i, j + 1);}}dfs(0, 0);return num;};function canMove(i, j, k) {let vali = i.toString().split('').reduce((a, b) => {return Number(a) + Number(b);});let valj = j.toString().split('').reduce((a, b) => {return Number(a) + Number(b);});if (Number(vali) + Number(valj) <= k) return true;return false;}
括号生成
描述
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例
输入:n = 3输出:["((()))","(()())","(())()","()(())","()()()"]
分析
看到这种符合某种规律,但又有区别的算法问题,自然想到递归的解法。当然我们也知道递归解法是可以转化为栈+循环的解法的。
观察可得:
- 某一次递归终止时需要将当前字符存入数组
- 字符任取一个位置左侧必为左括号 >= 右括号
- 每次递归除了需要传当前字符还需要记清当前左右括号数
代码
var generateParenthesis = function(n) {let res = [];// cur :当前字符 left:当前字符左括号 right:当前字符右括号const help = (cur, left, right) => {if (cur.length === 2 * n) {res.push(cur);return;}if (left < n) {help(cur + '(', left + 1, right);}if (right < left) {help(cur + ')', left, right + 1);}};help('', 0, 0);return res;};
翻转字符串里的单词
描述
给定一个字符串,逐个翻转字符串中的每个单词。
示例 1
输入: "the sky is blue"输出: "blue is sky the"
示例 2
输入: " hello world! "输出: "world! hello"解释: 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
示例 3
输入: "a good example"输出: "example good a"解释: 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
代码
/*** @param {string} s* @return {string}*/var reverseWords = function(s) {return s.split(' ').filter(item => item).reverse().join(' ');};
鸡蛋掉落
描述
你将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。
你知道存在楼层 F ,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?
示例 1
输入:K = 1, N = 2输出:2解释:鸡蛋从 1 楼掉落。如果它碎了,我们肯定知道 F = 0 。否则,鸡蛋从 2 楼掉落。如果它碎了,我们肯定知道 F = 1 。如果它没碎,那么我们肯定知道 F = 2 。因此,在最坏的情况下我们需要移动 2 次以确定 F 是多少。
示例 2
输入:K = 2, N = 6输出:3
示例 3
输入:K = 3, N = 14输出:4
提示:
1 <= K <= 1001 <= N <= 10000
代码
/*** @param {number} K* @param {number} N* @return {number}*/var superEggDrop = function(K, N) {let dp = Array(K + 1).fill(0);let cnt = 0;while (dp[K] < N) {cnt++;for (let i = K; i > 0; i--) {dp[i] = dp[i - 1] + dp[i] + 1;}}return cnt;};
设计推特
描述
设计一个简化版的推特(Twitter),可以让用户实现发送推文,关注/取消关注其他用户,能够看见关注人(包括自己)的最近十条推文。你的设计需要支持以下的几个功能:
postTweet(userId, tweetId): 创建一条新的推文
getNewsFeed(userId): 检索最近的十条推文。每个推文都必须是由此用户关注的人或者是用户自己发出的。推文必须按照时间顺序由最近的开始排序。
follow(followerId, followeeId): 关注一个用户
unfollow(followerId, followeeId): 取消关注一个用户
示例
Twitter twitter = new Twitter();// 用户1发送了一条新推文 (用户id = 1, 推文id = 5).twitter.postTweet(1, 5);// 用户1的获取推文应当返回一个列表,其中包含一个id为5的推文.twitter.getNewsFeed(1);// 用户1关注了用户2.twitter.follow(1, 2);// 用户2发送了一个新推文 (推文id = 6).twitter.postTweet(2, 6);// 用户1的获取推文应当返回一个列表,其中包含两个推文,id分别为 -> [6, 5].// 推文id6应当在推文id5之前,因为它是在5之后发送的.twitter.getNewsFeed(1);// 用户1取消关注了用户2.twitter.unfollow(1, 2);// 用户1的获取推文应当返回一个列表,其中包含一个id为5的推文.// 因为用户1已经不再关注用户2.twitter.getNewsFeed(1);
代码
/*** Initialize your data structure here.*/var Twitter = function() {this.time = 0;this.users = {}; // follows};/*** Compose a new tweet.* @param {number} userId* @param {number} tweetId* @return {void}*/Twitter.prototype.postTweet = function(userId, tweetId) {this.time += 1;let { users } = this;if (users[userId] === undefined) users[userId] = [];if (users[userId]['tweets'] === undefined) users[userId]['tweets'] = [];// 考虑重复推文let hasTweets = [];for (let tweet of users[userId]['tweets']) {hasTweets.push(tweet.tweetId);}if (hasTweets.includes(tweetId)) return;users[userId]['tweets'].push({ tweetId, time: this.time });};/*** Retrieve the 10 most recent tweet ids in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user herself. Tweets must be ordered from most recent to least recent.* @param {number} userId* @return {number[]}*/Twitter.prototype.getNewsFeed = function(userId) {let users = this.users,list = [],ids = [userId]; // 自己和自己关注的 userIdif (users[userId] === undefined) return [];let follows = users[userId]['follows'];if (follows !== undefined) {ids.push(...follows);}for (let userid of ids) {if (users[userid] === undefined) continue;if (users[userid]['tweets'] === undefined) continue;list.push(...users[userid]['tweets']);}list.sort((a, b) => b.time - a.time);let res = new Set(); // 去重重复推文,防止自己关注自己的情况for (let i = 0; i < list.length; i++) {res.add(list[i]['tweetId']);if (res.size === 10) break;}return [...res];};/*** Follower follows a followee. If the operation is invalid, it should be a no-op.* @param {number} followerId* @param {number} followeeId* @return {void}*/Twitter.prototype.follow = function(followerId, followeeId) {let users = this.users;if (users[followerId] === undefined) users[followerId] = [];if (users[followerId]['follows'] === undefined) {users[followerId]['follows'] = [];}if (users[followerId]['follows'].indexOf(followeeId) !== -1) return;users[followerId]['follows'].push(followeeId);};/*** Follower unfollows a followee. If the operation is invalid, it should be a no-op.* @param {number} followerId* @param {number} followeeId* @return {void}*/Twitter.prototype.unfollow = function(followerId, followeeId) {let users = this.users;if (users[followerId] === undefined) return;if (users[followerId]['follows'] === undefined) return;let userFollows = users[followerId]['follows'];let index = userFollows.indexOf(followeeId);if (index === -1) return;userFollows.splice(index, 1);};
两数相加 II
描述
给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
你可以假设除了数字 0 之外,这两个数字都不会以零开头。
示例
输入:(7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)输出:7 -> 8 -> 0 -> 7
分析
此题为两数之和的变体,两数之和是链表从根节点向后遍历相加,而此题是从后往前相加进位。很容易想到的思路是:将链表先旋转,求和后在旋转回去。这里我们必须联想到,栈 对于数据处理的一个优势,栈元素始终是后进先出,因此我们可以将两个链表各节点数字入栈,待 l1 入栈 stack1 , l2 入栈 stack2 完毕后,出栈求解两数之和从而生成新的链表节点,并连接成链表。
代码
/*** Definition for singly-linked list.* function ListNode(val) {* this.val = val;* this.next = null;* }*//*** @param {ListNode} l1* @param {ListNode} l2* @return {ListNode}*/var addTwoNumbers = function(l1, l2) {let stack1 = [];let stack2 = [];while (l1) {stack1.push(l1.val);l1 = l1.next;}while (l2) {stack2.push(l2.val);l2 = l2.next;}let mark = 0;let res = null;while (stack1.length > 0 || stack2.length > 0 || mark !== 0) {let val1 = stack1.length > 0 ? stack1.pop() : 0;let val2 = stack2.length > 0 ? stack2.pop() : 0;let val = val1 + val2 + mark;mark = (val / 10) | 0;curNode = new ListNode(val % 10);curNode.next = res;res = curNode;}return res;};
01 矩阵
描述
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入0 0 00 1 00 0 0输出0 0 00 1 00 0 0
示例 2:
输入0 0 00 1 01 1 1输出0 0 00 1 01 2 1
注意:
- 给定矩阵的元素个数不超过 10000。
- 给定矩阵中至少有一个元素是 0。
- 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
分析
典型的动态规划问题
代码
/*** @param {number[][]} matrix* @return {number[][]}*/var updateMatrix = function(matrix) {// dp optimiseif (matrix.length == 0) {return [];}let m = matrix.length,n = matrix[0].length;// left-top to right-bottomfor (let i = 0; i < m; i++) {for (let j = 0; j < n; j++) {if (matrix[i][j] != 0) {matrix[i][j] = m + n;if (i > 0) {matrix[i][j] = Math.min(matrix[i - 1][j] + 1, matrix[i][j]);}if (j > 0) {matrix[i][j] = Math.min(matrix[i][j - 1] + 1, matrix[i][j]);}}}}// right-bottom to left-topfor (let i = m - 1; i >= 0; i--) {for (let j = n - 1; j >= 0; j--) {// distanceif (matrix[i][j] != 0) {if (j < n - 1) {matrix[i][j] = Math.min(matrix[i][j], matrix[i][j + 1] + 1);}if (i < matrix.length - 1) {matrix[i][j] = Math.min(matrix[i][j], matrix[i + 1][j] + 1);}}}}return matrix;};
合并区间
描述
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: [[1,3],[2,6],[8,10],[15,18]]输出: [[1,6],[8,10],[15,18]]解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: [[1,4],[4,5]]输出: [[1,5]]解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
分析
很多场景可能用到这个算法,比如时间区间的合并。
代码
/*** @param {number[][]} intervals* @return {number[][]}*/var merge = function(intervals) {if (!intervals || !intervals.length) return [];intervals.sort((a, b) => a[0] - b[0]);let ans = [intervals[0]];for (let i = 1; i < intervals.length; i++) {if (ans[ans.length - 1][1] >= intervals[i][0]) {ans[ans.length - 1][1] = Math.max(ans[ans.length - 1][1],intervals[i][1],);} else {ans.push(intervals[i]);}}return ans;};
跳跃游戏
描述
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]输出: true解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4]输出: false解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
分析
我们可以使用贪心算法来解该题,一直向后匹配,直至不满足条件位置。定义一个存储当前跳转到下一元素的数字,如果遍历过程中,索引大于了该数字,表示无法跳到最后。示例 2 的例子,当跳到 0 位置时,此时 k = 3, i = 3,到下一个位置,k = 3, i = 4,i > k 成立,返回 false。
代码
/*** @param {number[]} nums* @return {boolean}*/var canJump = function(nums) {let k = 0;for (let i = 0; i < nums.length; i++) {if (i > k) return false;k = Math.max(k, i + nums[i]);}return true;};
盛最多水的容器
描述
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
**说明:**你不能倾斜容器,且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 :
输入:[1,8,6,2,5,4,8,3,7]输出:49
分析
本题解法类似 盛雨水 ,使用双指针。
代码
/*** @param {number[]} height* @return {number}*/var maxArea = function(height) {let i = 0,j = height.length - 1;let square,max = 0;while (j - i >= 1) {if (height[i] > height[j]) {square = height[j] * (j - i);j--;} else {square = height[i] * (j - i);i++;}max = Math.max(square, max);}return max;};
岛屿数量
描述
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:11110110101100000000输出: 1
示例 2:
输入:11000110000010000011输出: 3解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
分析
我们其实就是要求红色区域的个数,换句话说就是求连续区域的个数。
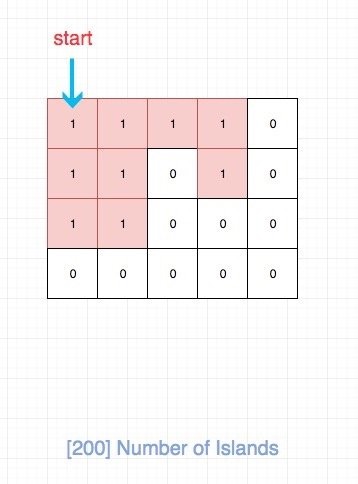
可以运用深度优先搜索(DFS)来解。
- 建立一个 visited 数组用来记录某个位置是否被访问过;
- 对于一个为
1且未被访问过的位置,我们递归进入其上下左右位置上为1的数,将其 visited 变成 true; - 重复以上步骤;
- 找完相邻区域后,我们将结果 res 自增 1,然后我们在继续找下一个为
1且未被访问过的位置,直至遍历完;
代码
/** @lc app=leetcode id=200 lang=javascript** [200] Number of Islands*/function helper(grid, i, j, rows, cols) {if (i < 0 || j < 0 || i > rows - 1 || j > cols - 1 || grid[i][j] === '0')return;grid[i][j] = '0';helper(grid, i + 1, j, rows, cols);helper(grid, i, j + 1, rows, cols);helper(grid, i - 1, j, rows, cols);helper(grid, i, j - 1, rows, cols);}/*** @param {character[][]} grid* @return {number}*/var numIslands = function(grid) {let res = 0;const rows = grid.length;if (rows === 0) return 0;const cols = grid[0].length;for (let i = 0; i < rows; i++) {for (let j = 0; j < cols; j++) {if (grid[i][j] === '1') {helper(grid, i, j, rows, cols);res++;}}}return res;};
统计「优美子数组」
描述
给你一个整数数组 nums 和一个整数 k。
如果某个 连续 子数组中恰好有 k 个奇数数字,我们就认为这个子数组是**「优美子数组」**。
请返回这个数组中**「优美子数组」**的数目。
示例 1:
输入:nums = [1,1,2,1,1], k = 3输出:2解释:包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。
示例 2:
输入:nums = [2,4,6], k = 1输出:0解释:数列中不包含任何奇数,所以不存在优美子数组。
示例 3:
输入:nums = [2,2,2,1,2,2,1,2,2,2], k = 2输出:16
提示:
1 <= nums.length <= 500001 <= nums[i] <= 10^51 <= k <= nums.length
分析
巧妙解法,详细直接上代码。
代码
/*** @param {number[]} nums* @param {number} k* @return {number}*/const numberOfSubarrays = (nums, k) => {let n = nums.length,counts = new Array(n + 1).fill(0).fill(1, 0, 1),oddCount = 0,result = 0;for (let i = 0; i < n; i++) {oddCount += nums[i] & 1;result += oddCount >= k ? counts[oddCount - k] : 0;counts[oddCount] += 1;}return result;};
二叉树的右视图
描述
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 :
输入: [1,2,3,null,5,null,4]输出: [1, 3, 4]解释:1 <---/ \2 3 <---\ \5 4 <---
分析
典型二叉树的遍历问题,可以使用递归深度优先搜索实现,转自 LeetCode

代码
/*** Definition for a binary tree node.* function TreeNode(val) {* this.val = val;* this.left = this.right = null;* }*//*** @param {TreeNode} root* @return {number[]}*/var rightSideView = function(root) {if (!root) return [];let arr = [];dfs(root, 0, arr);return arr;};function dfs(root, step, res) {if (root) {if (res.length === step) {res.push(root.val); // 当数组长度等于当前 深度 时, 把当前的值加入数组}dfs(root.right, step + 1, res); // 先从右边开始, 当右边没了, 再轮到左边dfs(root.left, step + 1, res);}}
硬币
描述
硬币。给定数量不限的硬币,币值为 25 分、10 分、5 分和 1 分,编写代码计算 n 分有几种表示法。(结果可能会很大,你需要将结果模上 1000000007)
示例 1 :
输入: n = 5输出:2解释: 有两种方式可以凑成总金额:5=55=1+1+1+1+1
示例 2 :
输入: n = 10输出:4解释: 有四种方式可以凑成总金额:10=1010=5+510=5+1+1+1+1+110=1+1+1+1+1+1+1+1+1+1
说明:
注意:
你可以假设:
- 0 <= n (总金额) <= 1000000
分析
本题可使用动态规划或数学解法求解,以动态规划为例。
代码
/*** @param {number} n* @return {number}*/let waysToChange = n => {let dp = new Array(n + 1).fill(1);let coins = [1, 5, 10, 25];for (let i = 1; i < 4; i++) {for (let j = 1; j <= n; j++) {if (j - coins[i] >= 0) {dp[j] = (dp[j] + dp[j - coins[i]]) % (1e9 + 7);}}}return dp[n];};
数组中的逆序对
描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 :
输入: [7,5,6,4]输出: 5
限制:
0 <= 数组长度 <= 50000
分析
首先能想到使用暴力解法,双重循环,但时间复杂度为 N 方,显然有待改进。
可使用归并的方式实现
代码
/*** @param {number[]} nums* @return {number}*/var reversePairs = function(nums) {// 归并排序let sum = 0;mergeSort(nums);return sum;function mergeSort(nums) {if (nums.length < 2) return nums;const mid = parseInt(nums.length / 2);let left = nums.slice(0, mid);let right = nums.slice(mid);return merge(mergeSort(left), mergeSort(right));}function merge(left, right) {let res = [];let leftLen = left.length;let rightLen = right.length;let len = leftLen + rightLen;for (let index = 0, i = 0, j = 0; index < len; index++) {if (i >= leftLen) res[index] = right[j++];else if (j >= rightLen) res[index] = left[i++];else if (left[i] <= right[j]) res[index] = left[i++];else {res[index] = right[j++];sum += leftLen - i; //在归并排序中唯一加的一行代码}}return res;}};
合并 K 个排序链表
描述
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例 :
输入:[1->4->5,1->3->4,2->6]输出: 1->1->2->3->4->4->5->6
分析
实现思路很多,比如:
- 双指针+合并
- 递归 + 分治
- 优先级队列
- 转换为数组求解
我们以递归+分支思路为例
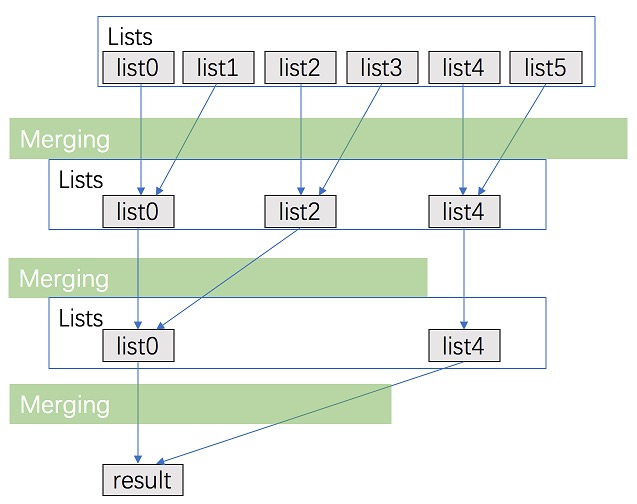
代码
/*** Definition for singly-linked list.* function ListNode(val) {* this.val = val;* this.next = null;* }*//*** @param {ListNode[]} lists* @return {ListNode}*/var mergeKLists = function(lists) {let n = lists.length;if (n == 0) return null;let mergeTwoLists = (l1, l2) => {if (l1 == null) return l2;if (l2 == null) return l1;if (l1.val <= l2.val) {l1.next = mergeTwoLists(l1.next, l2);return l1;} else {l2.next = mergeTwoLists(l1, l2.next);return l2;}};let merge = (left, right) => {if (left == right) return lists[left];let mid = (left + right) >> 1;let l1 = merge(left, mid);let l2 = merge(mid + 1, right);return mergeTwoLists(l1, l2);};return merge(0, n - 1);};
搜索旋转排序数组
描述
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例 1 :
输入: nums = [4,5,6,7,0,1,2], target = 0输出: 4
示例 2:
输入: nums = [4,5,6,7,0,1,2], target = 3输出: -1
分析
使用二分法即可完成,当然 JavaScript 中的数组方法 index 已实现该功能,见代码二。
代码
/*** @param {number[]} nums* @param {number} target* @return {number}*/var search = function(nums, target) {let l = 0;let r = nums.length - 1;while (l <= r) {let mid = l + ((r - l) >> 1); // 取中间索引if (nums[mid] === target) return mid; // 找到了 直接返回if (nums[l] <= nums[mid]) {// 如果第一个元素 小于等于 中间元素 表示 左边的是增序的 如[4,5,6,7,0,1,2]// 如果target 小于 中间元素, 大于第一个元素 ,说明target处于 [l, mid]间if (nums[mid] > target && nums[l] <= target) {r = mid - 1;} else {// 否则处于 [mid + 1, r]中l = mid + 1;}} else {// 否则 右边是增序的 如[6,7,0,1,2,4,5]// 如果target 大于中间元素 小于最后元素, 说明处于[mid + 1, r]中if (nums[mid] < target && nums[r] >= target) {l = mid + 1;} else {// 否则处于[l, mid - 1]中r = mid - 1;}}}// 没找到return -1;};
代码二
var search = function(nums, target) {return nums.indexOf(target);};
数组中数字出现的次数
描述
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是 O(n),空间复杂度是 O(1)。
示例 1 :
输入:nums = [4,1,4,6]输出:[1,6] 或 [6,1]
示例 2:
输入:nums = [1,2,10,4,1,4,3,3]输出:[2,10] 或 [10,2]
限制:
2 <= nums <= 10000
分析
hash 表解决这个问题很简单,见代码。
代码
var singleNumbers = function(nums) {var obj = {};nums.forEach(count => {let attr = count + '';obj[attr] ? delete obj[attr] : (obj[attr] = 1);});return Object.keys(obj);};
山脉数组中查找目标值
描述
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是 O(n),空间复杂度是 O(1)。
这是一个 交互式问题 )
给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。
如果不存在这样的下标 index,就请返回 -1。
何为山脉数组?如果数组 A 是一个山脉数组的话,那它满足如下条件:
首先,A.length >= 3
其次,在 0 < i < A.length - 1 条件下,存在 i 使得:
A[0] < A[1] < ... A[i-1] < A[i] A[i] > A[i+1] > ... > A[A.length - 1]
你将 不能直接访问该山脉数组,必须通过 MountainArray 接口来获取数据:
MountainArray.get(k) - 会返回数组中索引为 k 的元素(下标从 0 开始) MountainArray.length() - 会返回该数组的长度
注意:
对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
分析
分作两步就清晰好多了:
- 把峰值找出來
- 按峰值把其分为左右两部分,先二分查找左边,左边没有再看右边
代码
/*** @param {number} target* @param {MountainArray} mountainArr* @return {number}*/var findInMountainArray = function(target, mountainArr) {// 一 查找峰值let left = 0;let right = mountainArr.length() - 1;let mid = left + ((right - left) >> 1);while (left <= right) {if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {// 当mid小于右边的时,说明峰值在右边, 继续在右边查找left = mid + 1;} else {// 否则在左边, 继续在左边查找right = mid - 1;}mid = left + ((right - left) >> 1);}// 执行完上边的二分查找 left 就是峰值的下标了// 二 根据峰值分两段 二分查找let res = -1;res = binarySearch(mountainArr, 0, left, target, true);res === -1 &&(res = binarySearch(mountainArr,left,mountainArr.length() - 1,target,false,));return res;};/*** @param {MountainArray} mountainArr* @param {number} left* @param {number} right* @param {number} target* @param {Boolean} isUp* @return {number}*/function binarySearch(mountainArr, left, right, target, isUp) {let mid = left + ((right - left) >> 1); // 获取中间索引while (left <= right) {let midValue = mountainArr.get(mid);if (midValue === target) return mid; // 找到直接返回if (midValue < target) {isUp ? (left = mid + 1) : (right = mid - 1); //用 isUp 区分正序还是降序} else {isUp ? (right = mid - 1) : (left = mid + 1);}mid = left + ((right - left) >> 1);}return -1;}
快乐数
描述
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
分析
在一些场景, 如链表数据结构和判断循环, 利用快慢指针创造的差值, 可节省内存空间, 减少计算次数
代码
var isHappy = function(n) {let slowPointer = n;let fastPointer = n;function getBitSquareSum(n) {let sum = 0;while (n !== 0) {const bit = n % 10;sum += bit * bit;n = parseInt(n / 10);}return sum;}do {slowPointer = getBitSquareSum(slowPointer);fastPointer = getBitSquareSum(getBitSquareSum(fastPointer));} while (slowPointer !== fastPointer);return slowPointer === 1;};